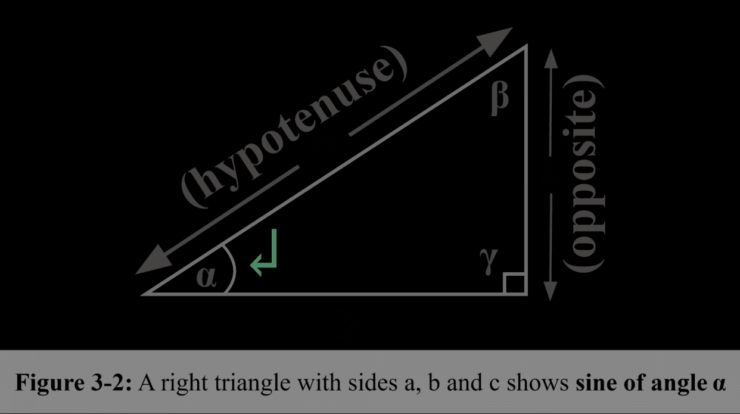
Sine meaning, a cornerstone of trigonometry, delves into the mathematical concept that defines the ratio of the opposite side to the hypotenuse in a right triangle. Its multifaceted nature extends beyond mere definition, encompassing properties, applications, and a rich historical tapestry.

Sine’s mathematical representation, graphical interpretation, and algebraic formulation lay the groundwork for understanding its behavior across different quadrants. Its periodicity, amplitude, and range unveil its characteristic patterns.

Definition and Meaning

The sine function, denoted as sin(x), is a mathematical function that measures the vertical coordinate of a point on a unit circle as an angle x radians from the positive x-axis. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle with one angle equal to x.

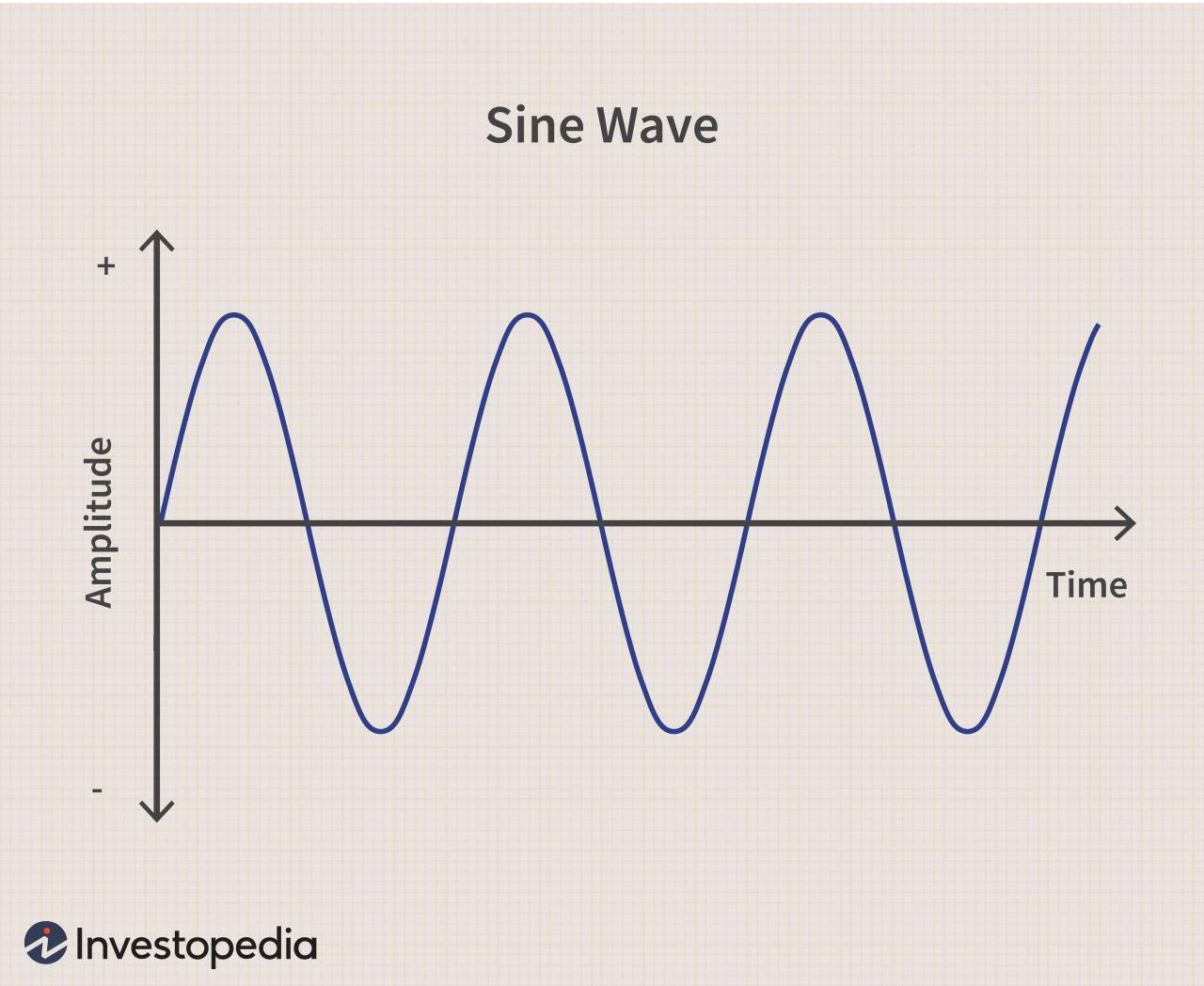
The sine function can also be represented graphically as a wave that oscillates between -1 and 1. The period of the sine wave is 2π, meaning that it repeats every 2π radians or 360 degrees.

Properties of Sine

The sine function has several key properties:

• Periodicity:The sine function repeats itself every 2π radians.
• Amplitude:The maximum and minimum values of the sine function are 1 and -1, respectively.
• Range:The range of the sine function is [-1, 1].

The sine function is also related to other trigonometric functions, such as cosine and tangent, by the following identities:

• sin(x) = cos(π/2 – x)
• tan(x) = sin(x) / cos(x)

Applications of Sine

The sine function has a wide range of applications in various fields, including:

• Physics:The sine function is used to model simple harmonic motion, such as the motion of a pendulum or a spring.
• Engineering:The sine function is used to analyze the vibrations of structures, such as bridges and buildings.
• Music:The sine function is used to create musical tones, such as those produced by a guitar string or a flute.

Historical Development of Sine, Sine meaning

The concept of sine was first developed by ancient Greek mathematicians, such as Hipparchus and Ptolemy. They used the sine function to calculate the lengths of chords in circles and to solve astronomical problems.

In the 16th century, the sine function was further developed by European mathematicians, such as Leonhard Euler and Isaac Newton. They developed the calculus of trigonometric functions, which allowed them to study the properties of the sine function in more detail.

Closure

From physics to engineering and music, sine finds practical applications in modeling real-world phenomena, such as sound waves and projectile motion. Its role in signal processing and data analysis underscores its significance in modern technology.

Questions Often Asked: Sine Meaning

What is the sine of an angle?

Sine is the ratio of the opposite side to the hypotenuse in a right triangle.

How is sine represented graphically?

Sine is represented as a wave that oscillates between -1 and 1.

What are the key properties of sine?

Periodicity, amplitude, and range are the key properties of sine.

What are some applications of sine?

Sine is used in physics, engineering, music, signal processing, and data analysis.